比赛链接

虽然让找 ，但枚举 很没前途啊，所以考虑找到所有 的个数

发现对于一组合法的 需要满足

那么我们对于每一个 ，找到所有的 使得 ，查分维护区间

时间复杂度为调和级数级别的

题解单飞咯！

题解链接

下发题解说的神马东西，赛时根本想不到

讲一个赛时想得到的 的思路，很好理解

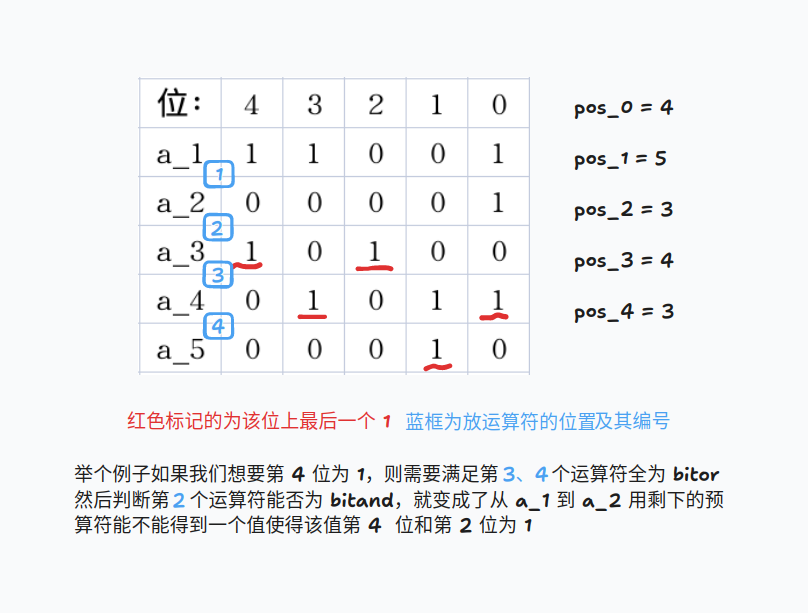
我们处理出二进制下每一位上的 1 的最后一次出现的位置，将第 位上的 1 最后一次出现的位置记作

同时我们设 为总共有的 的操作数

有以下结论：由于 是 位上最后一个 1，所以一旦它后面放了一个 与，这一位上就是 0 了；若我们想要这一位为 1，必须至少满足从 到最后的运算符全是 。

发现有以下情况：

• 若 ，即 之后需要放的运算符的数量比 的总操作数多，也就是说在 之后我一定需要放 操作，所以这种情况下这一位一定不对答案有贡献

• 若 ，也就是说我可以从 的前一个位置开始到最后全放 操作，那么这样第 位上可以是 1，为了使值最大，所以第 位上一定要是 1，所以从第 位到最后必须全是 操作，对于这种情况的 我们记为合法位

• 若 ，也就是说从第 到最后的运算符可以全是 操作，但 的前一位只能是
  所以我们特判从第 1 个位置到 的前一位全放 能不能让到第 个数时得到的值第 $forall $ 位为 1，若能则该位也为合法位，否则不合法

对于所有合法位的 取最小值设为 ，因为已经保证 到最后的预算符全是 ，此时有一下两种可能，而我们想尽量构成第二种可能：

1. 的前一位预算符也为 ，这样我们一定能达到答案最大了，想使答案最优直接让从 开始的 个运算符为 就好了

2. 的前一位在某些情况为 也是可以使答案最大的，所以我们判断能不能让 的前一位为 同样使答案最大；
   发现可以的条件相当于从第 个数到最前面用仅剩的 操作得到一个答案，使得这个答案第 $forall $ 位为 1，若能满足条件则第 个操作符为 。

满足条件的判断又和上述的第三个情况判断一致了，相当于以 为下界，再做一次求 ，实质上是不断的递归。

形式化如下：

所以一个递归 表示下界为 ，还剩 个 操作，判断能不能得到我想要的答案：

若不能则直接从第 开始的 个运算符全为 就是答案（ 为在之前的递归中已经确定的 的个数）

若能则第 个位置可以为 ，并设 ，继续递归 判断第 个位置能不能为 。